Определение силы сопротивления в физике и её формула

Разновидности сил сопротивления

Существуют такие разновидности сил сопротивления:

1. Сила сопротивления качению $P_f$, зависимая от таких факторов, как: разновидности и состояния опорной поверхности, скорости движения, давления воздуха и пр. Коэффициент сопротивления качению $f$ зависеть при этом состояния и типа опорной поверхности. С повышением температуры и давления, указанный коэффициент уменьшается.
2. Сила сопротивления воздуха (лобовое сопротивление) $Р_в$ возникает за счет разницы давлений. Данный показатель окажется тем выше, чем большим будет вихреобразование как в передней, так и в задней части объекта движения. Величина вихреобразования будет зависеть от формы движущихся тел.

Наиболее значимым будет воздействие на сопротивление движению передней части. Так, при создании закругления в передней и задней части плоскостенной фигуры, сопротивление возможно уменьшить на 72 %. Сила лобового сопротивления $Р_{вл}$ определяется по такой формуле:

$P_{вл} = {c_xpF_в}\frac{v^2}{2}$, где:

• $с_х$– коэффициент лобового сопротивления (обтекаемости);
• $p$- плотность воздуха;
• $F_в$ –площадь лобового сопротивления (миделевого сечения) определяется по формуле

Сила сопротивления воздуха ориентирована в направлении, противоположном вектору скорости объекта движения (например, автомобиля). Обычно она рассматривается как сконцентрированная сила, приложенная в отношении точки (центра парусности объекта), не совпадающей при этом с центром массы исследуемого объекта.

Сила сопротивления разгону поступательно движущейся массы объекта, согласно второму закону Ньютона, определяется таким образом:

$Рj = m\frac{dV}{dt}$, где:

• $m$– масса автомобиля;
• $\frac{dv}{dt}$ — ускорение центра масс.

Очень низкие числа Рейнольдса: сопротивление Стокса

Траектории трех объектов, брошенных под одинаковым углом (70 °). Черный объект не испытывает никакого сопротивления и движется по параболе. Синий объект испытывает сопротивление Стокса , а зеленый объект — Ньютон .

Уравнение для вязкого сопротивления или линейного сопротивления подходит для объектов или частиц , проходящих через жидкость при относительно медленной скорости , где нет турбулентности (т.е. с низким числа Рейнольдса , )

Обратите внимание, что чисто ламинарный поток существует только до Re = 0,1 согласно этому определению. В этом случае сила сопротивления приблизительно пропорциональна скорости

Уравнение вязкого сопротивления:
ре

Fdзнак равно-бv{\ displaystyle \ mathbf {F} _ {d} = — b \ mathbf {v} \,}

где:

б{\ displaystyle \ mathbf {} b} — константа, которая зависит от свойств жидкости и размеров объекта, и

v{\ displaystyle \ mathbf {v}} это скорость объекта

Когда объект падает из состояния покоя, его скорость будет

v(т)знак равно(ρ-ρ)Vграммб(1-е-бтм){\ displaystyle v (t) = {\ frac {(\ rho — \ rho _ {0}) Vg} {b}} \ left (1-e ^ {- bt / m} \ right)}

которая асимптотически приближается к конечной скорости . Как известно , более тяжелые предметы падают быстрее.
vтзнак равно(ρ-ρ)Vграммб{\ Displaystyle \ mathbf {} v_ {t} = {\ frac {(\ rho — \ rho _ {0}) Vg} {b}}}б{\ displaystyle \ mathbf {} b}

Для частного случая небольших сферических объектов, медленно движущихся в вязкой жидкости (и, следовательно, при малом числе Рейнольдса), Джордж Габриэль Стокс вывел выражение для константы сопротивления:

бзнак равно6πηр{\ Displaystyle б = 6 \ пи \ эта г \,}

где:

р{\ displaystyle \ mathbf {} r}- радиус Стокса частицы, — вязкость жидкости.η{\ displaystyle \ mathbf {} \ eta}

Результирующее выражение для сопротивления известно как сопротивление Стокса :

Fdзнак равно-6πηрv.{\ displaystyle \ mathbf {F} _ {d} = — 6 \ pi \ eta r \, \ mathbf {v}.}

Например, рассмотрим небольшую сферу радиусом 0,5 мкм (диаметром 1,0 мкм), движущуюся через воду со скоростью 10 мкм / с. Используя 10 -3 Па · с в качестве динамической вязкости воды в единицах СИ, мы находим силу сопротивления 0,09 пН. Речь идет о силе сопротивления, которую испытывает бактерия, плавая в воде.
р{\ displaystyle \ mathbf {} r}v{\ displaystyle \ mathbf {} v}

Коэффициент сопротивления шара может быть определен для общего случая ламинарного течения с числами Рейнольдса меньше 1 по следующей формуле:
2⋅105{\ displaystyle 2 \ cdot 10 ^ {5}}

CDзнак равно24ре+4ре+0,4 ;     ре<2⋅105{\ displaystyle C_ {D} = {\ frac {24} {Re}} + {\ frac {4} {\ sqrt {Re}}} + 0,4 ~ {\ text {;}} ~~~~~ Re < 2 \ cdot 10 ^ {5}}

Для чисел Рейнольдса меньше 1 применяется закон Стокса и коэффициент сопротивления приближается !
24ре{\ displaystyle {\ frac {24} {Re}}}

3.12. Уравнение движения автомобиля

Для вывода уравнения
движения рассмотрим разгон автомоби­ля
на подъеме (рис. 3.21).

Спроецируем все
силы, действующие на автомобиль, на
по­верхность дороги:

(3.19)

Подставим
в формулу (3.19) касательные реакции дороги
R_x1,
и R_x2,

объединим
члены с коэффициентом сопротивления
каче­нию ƒ и члены с ускорением j
и, принимая во внимание соотно­шения
ƒ(Rz2+Rz1
) = РK,
и
jk1
+ jk2
= jk
, а также коэффициент уче­та вращающихся
масс, получим уравнение движения
автомобиля в общем виде:

Или

(3.20)

Уравнение движения
автомобиля выражает связь между
дви­жущими силами и силами сопротивления

Рис.
3.21. Схема сил, действую­щих
на автомобиль на подъеме

движению.
Оно позволяет определить режим движения
автомобиля в любой момент.

Так, например, при
установившемся (равномерном) движе­нии

Из уравнения (3.20)
следует, что безостановочное движение
автомобиля возможно только при условии

р

гв-

Данное неравенство
связыва­ет конструктивные параметры
ав­томобиля с эксплуатационными
факторами, обусловливающими сопротивление
движению. Одна­ко оно не гарантирует
отсутствия буксования ведущих колес.
Безо­становочное движение автомоби­ля
без буксования ведущих колес возможно
лишь при соблюдении условия

Условия
равномерного движения при отсутствии
буксования ведущих колёс записывается
в виде

Что ещё влияет на аэродинамику?

Конечно, конструкторы стараются по максимуму снизить сопротивление авто при движении и повысить прижимную силу. Но особенности эксплуатации авто и свой взгляд автовладельцев на внешние особенности машины вносят свои коррективы, причем в некоторых случаях – значительны.

Аэродинамическое сопротивление разных автомобилей в зависимости от скорости

К примеру, установка багажника на крышу, даже с аэродинамической формой увеличивает поперечную проекцию авто и сильно влияет на обтекаемость, это сразу сказывается на потреблении топлива.

Также расход повышается от езды с открытыми окнами и люком, использование защитных и декоративных обвесов, перевозка негабаритных грузов, выступающих за авто, нарушение положения конструктивных элементов, расположенных под днищем, повышение клиренса.

Но автовладелец также может и внести коррективы, которые положительно повлияют на аэродинамику автомобиля. К ним относится использование аэродинамических обвесов, установка спойлера, уменьшение клиренса.

Сила сопротивления дороги

Сила
сопротивления дороги представляет
собой сумму сил со­противления качению
и сопротивления подъему:

или

Выражение
в скобках, характеризующее дорогу в
общем слу­чае, называется коэффициентом
сопротивления дороги:

При
малых углах подъема (не превышающих
5°), характерных для большинства
автомобильных дорог с твердым покрытием,
ко­эффициент сопротивления дороги

Сила
сопротивления дороги в этом случае

Зная
силу сопротивления доро­ги, можно
определить мощность, кВт, необходимую
для его преодо­ления:

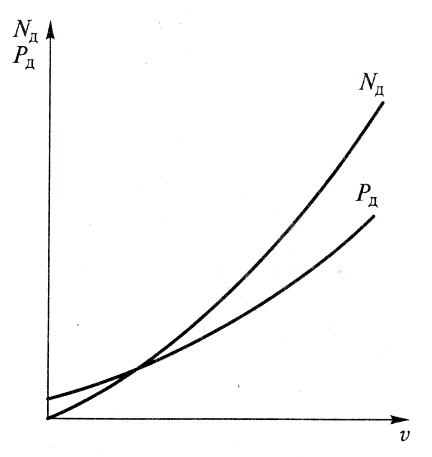Рис.
3.17. Зависимости силы сопро­тивления
дороги Р_д
и мощности N_д,
затрачиваемой
на его преодоление, от
скорости автомобиля

где
скорость автомобиля
выражена
в м/с, вес G
— в
Н, мощ­ность Nд
— в кВт.

Зависимости
силы сопротивления дороги Р_Д
и мощности
N_д,
затрачиваемой на его преодоление, от
скорости автомобиля
представлены
на рис. 3.17.

Скорости движения (а), давления воздуха в шине (б) и момента, передаваемого через колесо (в)

факторов
и определяется экспериментально. Его
средние значения для различных дорог
при нормальном давлении воздуха в шине
составляют 0,01 …0,1.Рассмотрим влияние
различных факторов на коэффициент
сопротивления качению.

Скорость
движения.
При изменении скорости движения в
ин­тервале 0…50 км/ч коэффициент
сопротивления качению изме­няется
незначительно и его можно считать
постоянным в указан­ном диапазоне
скоростей.

При
повышении скорости движения за пределами
указанного интервала коэффициент
сопротивления качению существенно
уве­личивается (рис. 3.15, а)
вследствие
возрастания потерь энергии в шине на
трение.

Коэффициент
сопротивления качению в зависимости
от ско­рости движения можно приближенно
рассчитать по
формуле

где
—
скорость
автомобиля, км/ч.

Тип
и состояние покрытия дороги.
На дорогах с твердым по­крытием
сопротивление качению обусловлено
главным образом деформациями шины.

При
увеличении числа дорожных неровностей
коэффициент сопротивления качению
возрастает.

На
деформируемых дорогах коэффициент
сопротивления ка­чению определяется
деформациями шины и дороги. В этом случае
он зависит не только от типа шины, но и
от глубины образую­щейся колеи и
состояния грунта.

Значения
коэффициента сопротивления качению
при рекомен­дуемых уровнях давления
воздуха и нагрузки на шину и средней
скорости движения на различных дорогах
приведены ниже:

Асфальто-
и цементобетонное шоссе:

в
хорошем состоянии
………………………………. 0,007…0,015

в
удовлетворительном состоянии
…………… 0,015…0,02

Гравийная
дорога в хорошем состоянии …. 0,02…0,025

Булыжная
дорога в хорошем состоянии…… 0,025…0,03

Грунтовая
дорога сухая, укатанная …………..
0,025…0,03

Песок…………………………………………………………..
0,1…0,3

Обледенелая
дорога, лед …………………………. 0,015…0,03

Укатанная
снежная дорога ………………………..
0,03…0,05

Тип
шины.
Коэффициент сопротивления качению во
многом зависит от рисунка протектора,
его износа, конструкции каркаса и
качества материала шины. Изношенность
протектора, уменьше­ние числа слоев
корда и улучшение качества материала
приводят к падению коэффициента
сопротивления качению вследствие
снижения потерь энергии в шине.

Давление
воздуха в шине.
На дорогах с твердым покрытием при
уменьшении давления воздуха в шине
коэффициент сопро­тивления качению
повышается (рис. 3.15, б).
На
деформируемых дорогах при снижении
давления воздуха в шине уменьшается
глу­бина колеи, но возрастают потери
на внутреннее трение в шине. Поэтому
для каждого типа дороги рекомендуется
определенное давление воздуха в шине,
при котором коэффициент сопротивле­ния
качению имеет минимальное значение.

Нагрузка
на колесо.
При увеличении вертикальной нагрузки
на колесо коэффициент сопротивления
качению существенно возрастает на
деформируемых дорогах и незначительно
— на до­рогах с твердым покрытием.

Момент,
передаваемый через колесо.
При передаче момента через колесо
коэффициент сопротивления качению
возрастает (рис. 3.15, в)
вследствие
потерь на проскальзывание шины в месте
ее контакта с дорогой. Для ведущих колес
значение коэффициента сопротивления
качению на 10… 15 % больше, чем для ведомых.

Коэффициент
сопротивления качению оказывает
существен­ное влияние на расход
топлива и, следовательно, на топливную
экономичность автомобиля. Исследования
показали, что даже не­большое уменьшение
этого коэффициента обеспечивает
ощути­мую экономию топлива. Поэтому
неслучайно стремление конст­рукторов
и исследователей создать такие шины,
при использова­нии которых коэффициент
сопротивления качению будет незна­чительным,
но это весьма сложная проблема.

Сила сопротивления воздуха

При
движении действие силы сопротивления
воздуха обуслов­лено перемещением
частиц воздуха и их трением о поверхность
автомобиля. Если он движется при
отсутствии ветра, то сила со­противления
воздуха, Н:

тогда
как при наличии ветра

где
k_в
— коэффициент
сопротивления воздуха (коэффициент
об­текаемости), Н-с2/м4;
F_а
— лобовая
площадь автомобиля, м2;

—
скорость
автомобиля, м/с;
_в
— скорость
ветра, м/с (знак «+» со­ответствует
встречному ветру, знак «-» — попутному).

Коэффициент
сопротивления воздуха, зависящий от
формы и качества поверхности автомобиля,

Рис.
3.18. Площади лобового сопротивления
легкового (а)
и
грузового(б)
автомобилей

Рис.
3.20. Зависимости силы сопротивления
разгону Р_ни
мощности
N_И,
необходимой для
преодоления этого сопро­тивления,
от скорости автомобиля

определяется
эксперимен­тально при продувке в
аэродинамической трубе.

Коэффициент
сопротивления воздуха, Н-с2/м4,
составляет 0, 2. ..0,35 для легковых
автомобилей, 0, 35. ..0, 4 — для автобусов и
0, 6. ..0, 7 — для грузовых автомобилей. При
наличии прицепов со­противление
воздуха увеличивается, так как возрастает
наружная поверхность трения и возникают
завихрения воздуха между
тягачомиприцепами.Приэтом45

каждый
прицеп вызывает увеличение коэффициента
k_в
в среднем на 15…25 %.

Лобовая
площадь автомобиля зависит от его типа
(рис. 3.18). Ее приближенное значение, м2,
можно вычислить по следующим фор­мулам:

— для
грузовых автомобилей и автобусов;

— для
легковых автомобилей,

где
B
— колея
колес автомобиля, м; Н_а
— наибольшая
высота автомобиля, м; В_а
— наибольшая
ширина автомобиля, м.

Мощность, кВт,
затрачиваемая на преодоление сопротивле­ния
воздуха:

—
отсутствии
ветра;

— при
наличии ветра.

Зависимости
силы сопротивления воздуха Р_Bи
мощности N_В,
необхо­димой для преодоления этого
сопро­тивления, от скорости автомобиля
vприведены
на рис. 3.19.

Примеры решения задач

ПРИМЕР 1

Задание

Максимальная скорость автомобиля на горизонтальном участке дороги равна при максимальной мощности его равной P. Коэффициент лобового сопротивления автомобиля C, а наибольшая площадь сечения в направлении, перпендикулярном скорости S. Автомобиль подвергся реконструкции, наибольшую площадь сечения в направлении, перпендикулярном скорости уменьшили до величины , оставив коэффициент сопротивления без изменения. Считайте силу трения о поверхность дороги неизменной, найдите какова максимальная мощность автомобиля, если его скорость на горизонтальном участке дороги стала равна

Плотность воздуха равна .

Решение

Сделаем рисунок.

Мощность автомобиля определим как:
где — сила тяги автомобиля.
Считая, что автомобиль на горизонтальном участке дороги движется с постоянной скоростью, запишем второй закон Ньютона в виде:
В проекции на ось X (рис.1), имеем:
Силу сопротивления, которую испытывает автомобиль, двигаясь в воздухе, выразим как:

Тогда мощность автомобиля можно записать:

Выразим из (1.5) силу трения автомобиля о дорогу:

Запишем выражение для мощности, но с изменёнными по условию задачи параметрами автомобиля:

Учтем, что сила трения автомобиля о дорогу не изменилась, и примем во внимание выражение (1.6):

Ответ

ПРИМЕР 2

Задание	Какова максимальная скорость шарика, который свободно падает в воздухе, если известны: плотность шарика (), плотность воздуха (), масса шарика (), коэффициент сопротивления C?
Решение	Сделаем рисунок. Запишем второй закон Ньютона для свободного падения шарика:

При движении любого предмета по поверхности или в воздухе возникают силы, препятствующие этому. Их называют силами сопротивления или трения. В этой статье мы расскажем, как найти силу сопротивления, и рассмотрим факторы, влияющие на нее.

Сопротивление движения в воздухе используется во время прыжков с парашютом. В результате возникающего трения между куполом и воздухом скорость движения парашютиста снижается, что позволяет без ущерба для жизни заниматься парашютным спортом.

Для определения силы сопротивления
воздуха
создайте условия, при которых тело начнет под действием силы тяжести двигаться равномерно и прямолинейно. Рассчитайте значение силы тяжести, оно будет равно силе сопротивления воздуха. Если тело движется в воздухе, набирая скорость, сила его сопротивления находится при помощи законов Ньютона, также силу сопротивления воздуха можно найти из закона сохранения механической энергии и специальных аэродинамических формул.

Решения

1. Масляная краска снизила коэффициент трения между колёсами и рельсами, что привело к пробуксовке, поезд не смог двигаться вперёд. Посыпав рельсы сажей, удалось решить проблему, так как коэффициент трения увеличился, и колёса перестали буксовать.
2. Санки находятся в движении, следовательно, на них будет действовать сила трения скольжения, численно равная Fтр. = μ ⋅ N, где N — сила реакции опоры, которая, при условии горизонтальной поверхности, равняется весу санок с мальчиком: N = m ⋅ g.  Получаем формулу Fтр. = μ ⋅ m ⋅ g  , откуда выразим искомую величину 

Ответ задачи зависит от того, сдвинется ли брусок под действием внешнего воздействия. Поэтому вначале узнаем значение силы, которую нужно приложить к бруску для скольжения. Это будет максимально возможная сила трения покоя, определяющаяся по формуле Fтр. = μ ⋅ N , где N = m ⋅ g (при условии горизонтальной поверхности). Подставляя значения, получаем, что Fтр. = 35 Н. Данное значение больше прикладываемой силы, следовательно брусок не сдвинется с места. Тогда сила трения покоя будет равна внешней силе: Fтр. = F = 25 H .

Сопротивление при нулевой подъёмной силе

Эта составляющая сопротивления не зависит от величины создаваемой подъёмной силы и складывается из профильного сопротивления крыла, сопротивления элементов конструкции самолёта, не вносящих вклад в подъёмную силу, и волнового сопротивления. Последнее является существенным при движении с около- и сверхзвуковой скоростью, и вызвано образованием ударной волны, уносящей значительную долю энергии движения. Волновое сопротивление возникает при достижении самолётом скорости, соответствующей критическому числу Маха, когда часть потока, обтекающего крыло самолёта, приобретает сверхзвуковую скорость. Критическое число М тем больше, чем больше угол стреловидности крыла, чем более заострена передняя кромка крыла и чем оно тоньше.

Сила сопротивления направлена против скорости движения, её величина пропорциональна характерной площади S, плотности среды ρ и квадрату скорости V:

F=CFρv22S{\displaystyle F=C_{F}{\frac {\rho v^{2}}{2}}S}

CF{\displaystyle C_{F}} — безразмерный аэродинамический коэффициент сопротивления, получается из критериев подобия, например, чисел Рейнольдса и Фруда в аэродинамике.

Определение характерной площади зависит от формы тела:

• в простейшем случае (шар) — площадь поперечного сечения;
• для крыльев и оперения — площадь крыла/оперения в плане;
• для пропеллеров и несущих винтов вертолётов — либо площадь лопастей, либо ометаемая площадь винта;
• для подводных объектов обтекаемой формы — площадь смачиваемой поверхности;
• для продолговатых тел вращения, ориентированных вдоль потока (фюзеляж, оболочка дирижабля) — приведённая волюметрическая площадь, равная V2/3, где V — объём тела.

Мощность, требуемая для преодоления данной составляющей силы лобового сопротивления, пропорциональна кубу скорости (P=F⋅V=CFρV32S{\displaystyle P=F\cdot V=C_{F}{\dfrac {\rho V^{3}}{2}}S}).

Направление силы трения

Сила трения скольжения всегда направлена противоположно скорости относительного движения соприкасающихся тел

Важно помнить, что на каждое из соприкасающихся тел действует своя сила трения

Бывают ситуации, когда сила трения не препятствует движению, а совсем наоборот.

Представьте, что на ленте транспортёра лежит чемодан. Лента трогается с места, и чемодан движется вместе с ней. Сила трения между лентой и чемоданом оказалась достаточной, чтобы преодолеть инерцию чемодана, и эти тела движутся как одно целое. На чемодан действует сила трения покоя, возникающая при взаимодействии соприкасающихся поверхностей, которая направлена по ходу движения ленты транспортёра.

 Если бы лента была абсолютно гладкой, то чемодан начал бы скользить по ней, стремясь сохранить своё состояние покоя. Напомним, что это явление называется инерцией.

Сила трения покоя, помогающая нам ходить и бегать, также направлена не против движения, а вперёд по ходу перемещения. При повороте же автомобиля  сила трения покоя и вовсе направлена к  центру окружности. 

Для того чтобы понять, как направлена сила трения покоя, нужно предположить, в каком направлении стало бы двигаться тело, будь поверхность идеально гладкой. Сила трения покоя в этом случае будет направлена как раз в противоположную сторону. Пример, лестница у стены.

Подъемная и прижимная сила

В результате неравномерного обтекания потоком воздуха автомобиля с разных сторон возникает разница в скорости его движения.

Действующие подъемная и прижимная силы

Автомобиль движется и рассекает поток воздуха, при этом часть этого потока уходит под авто и проходит под днищем, то есть движется практически по прямой. А вот верхней части потока приходится повторять форму кузова, и ей приходится проходить большее расстояние. Из-за этого возникает разница в скорости воздуха – верхняя часть движется быстрее нижней, проходящей под авто. А поскольку увеличение скорости сопровождается снижением давления, то под днищем образуется зона повышенного давления, которая приподнимает машину.

Проблем добавляет и лобовое сопротивление. Область повышенного давления воздушной массы перед машиной прижимает передок к дороге, в то время как разрежение и завихрения позади наоборот – способствуют приподнятию кузова. Подъемная сила, как и лобовое сопротивление, возрастает при увеличении скорости движения.

Негативным фактором от воздействия такой силы является ухудшение устойчивости авто при увеличении скорости и повышение вероятности ухода в занос.

Но эта сила может оказывать и положительное действие. При внесении корректив в конструкцию авто возможно преобразование подъемной силы в прижимную, которая будет обеспечивать лучшее сцепление с дорогой, устойчивость авто, его управляемость на высоких скоростях.

При этом для получения прижимной силы не требуется каких-либо отдельных решений. Все разработки, направленные на снижение коэффициента Сх также сказываются и на прижиме. К примеру, оптимизация формы задней части приводит к уменьшению завихрений и разрежения, из-за чего подъемная сила тоже снижается, а прижимная — повышается. Установка заднего спойлера действует таким же образом.

Уменьшение завихрений при установке спойлера

Боковые же силы при установлении аэродинамики автомобиля, особо в расчет не берутся, в силу того, что они не постоянны, а также значительного влияния на показатели авто не оказывают.

Но это все теория аэродинамики автомобиля. На практике все можно пояснить одним предложением — чем хуже аэродинамика, тем выше расход топлива.

Сила сопротивления движению тела в воде — SportWiki энциклопедия

Сила сопротивления движению тела в воде

Для тела человека, плывущего в воде, при его равномерной скорости полное гидродинамическое сопротивление имеет вид

Rx = KV2,

где Rx — суммарная величина сопротивления; V — скорость плавания, м/с; К — безразмерный коэффициент сопротивления, составляющими которого являются:

Cx(p/2)S,

где Сх — коэффициент обтекаемости, иногда называемый коэффициентом пропорциональности или коэффициентом лобового сопротивления; р — плотность воды; S — миделевое сечение, являющееся проекцией тела на плоскость, перпендикулярную направлению движения.

Коэффициент обтекаемости тела зависит от формы тела, соотношения его ширины и длины, величины и состояния поверхности и для человека колеблется в пределах 0,5 — 3.

Как видно из формулы, величина полного гидродинамического сопротивления прямо пропорциональна величине миделевого сечения. При плавании человека величина миделевого сечения постоянно изменяется. Наименьшая проекция будет в том случае, если тело занимает в воде горизонтальное положение. Величину миделевого сечения необходимо учитывать не только при выборе рационального положения тела, но и при выполнении рабочих и подготовительных движений. Пловец продвигается вперед, опираясь конечностями о воду и отталкиваясь от нее. Отталкивания будут тем более эффективными, чем больше они будут вызывать сопротивление своему движению, которое зависит от величины миделевого сечения.

Практически это достигается тем, что ладони во время гребка располагаются по возможности перпендикулярно направлению движения. Поэтому при выполнении гребковых движений конечностями для обеспечения продвижения тела вперед и, если необходимо, поддержания его в более высоком положении следует ориентировать гребущие поверхности так, чтобы их миделевое сечение достигало возможно большей величины.

После выполнения гребковых движений пловцу нужно совершать подготовительные движения. При плавании кролем на груди, на спине и дельфином подготовительные движения руками совершаются над поверхностью воды. Иное дело — при плавании брассом, когда подготовительное движение рук и ног необходимо выполнять под поверхностью воды. При таких движениях проекция на плоскость, перпендикулярную движению, должна быть наименьшей. Поэтому движение рук вперед брассисты выполняют с прижатыми к телу плечами и близко к поверхности воды, а сгибание тазобедренных суставов — быстро, чтобы уменьшить время действия сопротивления передней поверхностью бедра.

При движении тела человека в воде величина сопротивления растет пропорционально квадрату скорости. Если пловец увеличит скорость своего движения в 3 раза, то сопротивление возрастает в 9 раз.

Поскольку пловец движется неравномерно, поэтому при расчетах сопротивления в свободном плавании возникают затруднения, так как при ориентации на среднюю скорость дистанции появляются погрешности. Для того чтобы получить более точные данные общей величины сопротивления, измеряют скорость тела за очень короткий промежуток времени. Такая скорость называется мгновенной. Колебания мгновенной скорости как в одном цикле движения, так и на всей дистанции бывают весьма значительными. Например, внутрицикловая скорость при плавании брассом может изменяться от 0,4 до 1,8 м/с.

Подведём итоги

1. Сила трения покоя меняется от нуля до максимального значения 0 < Fтр.покоя < Fтр.пок.макс  в зависимости от внешнего воздействия.
2. Максимальная сила трения покоя почти равна силе трения скольжения, лишь немного её превышая. Можно приближенно считать, что Fтр. = Fтр.пок.макс 
3. Силу трения скольжения можно рассчитать по формуле Fтр. = μ ⋅ N,  где  μ — коэффициент трения, N — сила нормальной реакции опоры.
4. При равномерном прямолинейном скольжении по горизонтальной поверхности сила тяги равна силе трения скольжения Fтр. = Fтяги.
5. Коэффициент трения μ зависит от рода и степени обработки  поверхностей 0 < μ < 1 . 
6. При одинаковых силе нормального давления и коэффициенте трения сила трения качения всегда меньше силы трения скольжения.

Учите физику вместе с домашней онлайн-школой «Фоксфорда»! По промокоду PHYSICS72020 вы получите бесплатный доступ к курсу физики 7 класса, в котором изучается закон силы трения.